Eigentlich ist das mathematische Konzept zur Erstellung solcher Bilder ganz einfach, und es ist erstaunlich welch komplexe Strukturen dabei auftreten.
Die schwarzen Flächen kennzeichnen dabei die X-Werte und Y-Werte, für die folgende Rekursion nicht divergiert bzw. nicht über eine vorgegebene Grenze (|z|<a) wächst:
z₀ = ( x + iy ), z₁ = z₀² + ( x + iy ), ... , z_n = z_n-1² + ( x + iy ).
Es sind auch noch unzählige andere Rekursionen möglich, die obige jedoch ist die bekannteste.

Ich habe die Bilder mit "Mathematica for Students" erstellt.
Die jeweils angegebene Differenz bedeutet die Breite und Höhe des Ausschnitts, der mit einer Genauigkeit von 500×500 Punkten berechnet wurde.

Wenn Sie Interesse an einer ausführlichen Exkursion in die Welt des Apfelmännchens finden Sie hier Sammlungen von vielen Bildern Gallerie 1, Gallerie 2.

Hier können Sie ein paar künstlerische Fraktale bewundern.

Von Hartmut Neubauer-Stankiewicz aus Köln habe ich jetzt ein, von ihm entwickeltes, Java-Applet bekommen, mit dem man selber seine Reise durch die Welt der Mandelbrot- und auch der Julia-Menge ein wenig gestalten kann.
Sie können das Applet laufen lassen, wenn Ihr Browser Java 1.1 unterstützt (z.B. MS Internet Explorer 4.x oder Netscape Communicator 4.x oder höher): MandelDraw

	Apfelmännchen X-Koordinate Y-Koordinate Minimum -2,0 -1,25 Maximum 0,5 1,25 Differenz 2,5
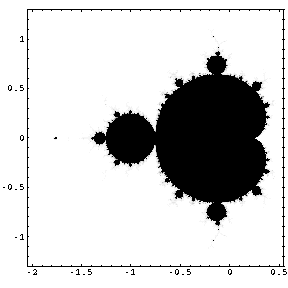
	Dies ist das ja schon vielen bekannte Apfelmännchen. Im folgenden soll nun eine kleine Reise in seine Struktur gemacht werden. Dazu wird zuerst ein Teil rechts vom "Hals" vergrößert und man kommt zu einem Ausschnitt mit "Rüsselmännchen", eine Seite weiter.

Auf dieser Seite gibt es noch drei weitere Bilder:

- Das erste Bild ist eine Vergrößerung des kleinen Flecks über dem Kopf, in dem man wiederum ein Apfelmännchen erkennt.

- Das zweite Bild ist eine Vergrößerung der kleinen Kugel in der Mitte zwischen dem "Kopf" und dem einen "Arm", die sich ebenfalls als eine Art Apfelmännchen zeigt.

- Das dritte Bild ist eine weitere Vergrößerung aus dem zweiten Bild und zeigt erneut ein Apfelmännchen.

-nach oben-

Spitze X-Koordinate Y-Koordinate Minimum -1,80 -0,035 Maximum -1,73 0,035 Differenz 0,07
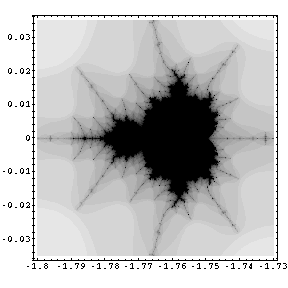
Dieses Bild zeigt eine Vergrößerung eines Apfelmännchens, das auf dem, aus dem Kopf der Ursprungsfigur herauskommenden Strahl liegt. Den Strahl kann man dort nur erahnen, da er an den meisten Stellen unendlich dünn ist. Auf diesem Bild läßt sich dieser Strahl mühelos ausmachen.

-nach oben-

Seite X-Koordinate Y-Koordinate Minimum -0,65 0,51 Maximum -0,45 0,71 Differenz 0,2

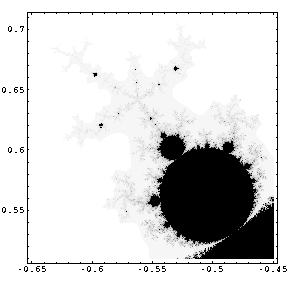
Dieses Bild zeigt eines von vielen Kugelmännchen, die sich rund um das Apfelmännchen verteilen. Sie sind sowohl am Körper sowie am Kopf - in verschiedenen Größen - zu finden. Weiterhin sieht man sie auch wieder an den Kugelmännchen selber. Über dem Kopf sieht man drei kleine Flecke, die wieder Apfelmännchen beinhalten. Das nächste Bild ist eine Vergrößerung eines dieser Flecken, und zwar die des unteren linken.

-nach oben-

Extra X-Koordinate Y-Koordinate Minimum -0,5975 0,615 Maximum -0,5875 0,625 Differenz 0,01
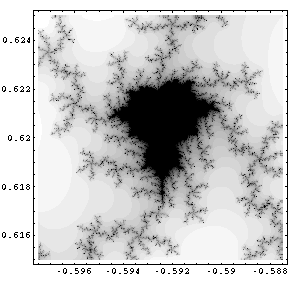
Dieses Bild zeigt eine weitere Variation der weit verbreiteten Apfelmännchen. In diesem Fall steht es auf dem Kopf. Ein besonderes Merkmal läßt sich an diesem Beispiel entdecken: Wenn die kleinen Apfelmännchen weit von der Urfigur und dessen Symetrieachse entfernt sind, dann sind sie oft etwas verzerrt. Es ist allerdings ziemlich schwer solche Exemplare aufzuspüren, da sie sehr klein sind.

-nach oben-

Bei Fragen oder Anregungen schreibt mir einfach eine Email.