Actually the mathematical concept for the creation of such pictures is completely simple, and it is amazing what complex structures origiate from that.
The black surfaces indicate thereby the x-values and y-values, for which the following recursion does not diverge or grows over a given boundary (|z|<a):
z₀ = ( x + iy ), z₁ = z₀² + ( x + iy ), ... , z_n = z_n-1² + ( x + iy ).
There are innumerable other recursions possible, as well, however the formula above is the most known version.

I created the pictures with "Mathematica for to Students".
The indicated difference in each case means the width and height of the window, which was calculated with an accuracy by 500×500 points.

If you are interested in a detailed study trip into the world of the Mandelbrot Set you'll here find a collection of several pictures Gallery 1, Gallery 2.

Here you can marvel some artistic fraktals.

From Hartmut Neubauer-Stankiewicz out of Köln I got a Java applet, he developed himself, with which you can arrange your own journey through the world of the Mandelbrot and also the Julia set.
You can make run the applet, if your Browser supports Java 1.1 (e.g. MS Internet Explorer 4.x oder Netscape Communicator 4.x or higher): MandelDraw

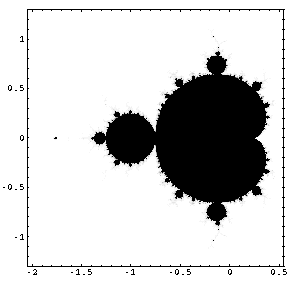
	Mandelbrot-Set X-Coordinate Y-Coordinate Minimum -2,0 -1,25 Maximum 0,5 1,25 Difference 2,5
	This is the figure of the already very well-known Mandelbrot-Set. Now, in the following a short journey is to be made into its structure. For that first a section on the right of the "neck" is enlarged and you reach a window with "trunk figures". next page

On this page there are three further pictures:

- The first picture is an enlargement of the small mark over the "head", in which you can detect a figure which also looks like the Mandelbrot-Set.

- The second picture is an enlargement of the small ball in the center between the "head" and one of the "arms", which likewise shows a figure like the Mandelbrot-Set.

- The third picture is a further enlargement from the second picture and again shows a figure like the Mandelbrot-Set.

-to the top-

Top X-Coordinate Y-Coordinate Minimum -1,80 -0,035 Maximum -1,73 0,035 Difference 0,07
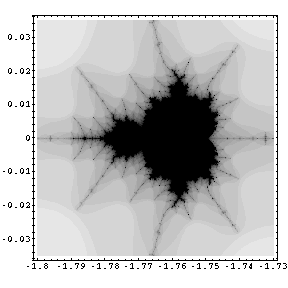
This picture shows an enlargement of the Mandelbrot-Set, which you can find on the jet coming out of the "head" of the origin figure. You hardly can suspect the jet there, since he is infinitely thin in most sections. In this picture that jet can be sighted easily.

-to the top-

Site X-Coordinate Y-Coordinate Minimum -0,65 0,51 Maximum -0,45 0,71 Difference 0,2

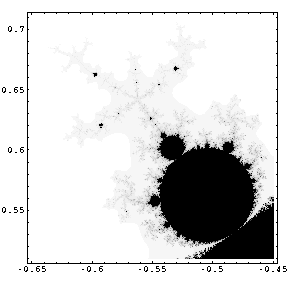
This picture shows one of many ball figures, which are distributed around the "body" of the Mandelbrot-Set. They can be found both at the "body" as well as at the "head" - in different sizes. Further you also see such figures again at the ball figures themselves. Above the "head" you see three small marks, which contain again figures like the Mandelbrot-Set. The next picture is an enlargement of one of this marks, to be precise of the lower left.

-to the top-

Extra X-Coordinate Y-Coordinate Minimum -0,5975 0,615 Maximum -0,5875 0,625 Difference 0,01

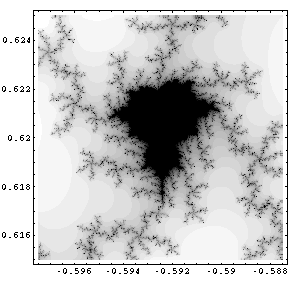
This picture shows a further variation of the wide-spread figures like the Mandelbrot-Set. In this case it is handstanding. A special feature can be discovered in this example: If the small figures like the Mandelbrot-Set are far away from the original figure and its symmetrical axis, then they are often somewhat distorted. However it is rather difficult to discover such copies, since they are very small.

-to the top-

In case of questions or suggestions just write an Email to me.